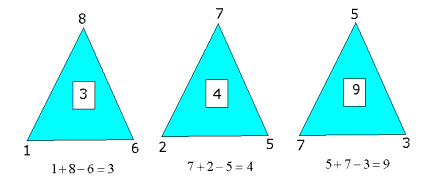
Adición y Sustracción
Este tipo de ejercitación me parece interesante trabajarla en el primer ciclo del E.G.B. Es una etapa donde los niños aprenden a través de actividades lúdicas.
El tipo de actividad que presento, es un sencillo ejemplo de cómo podemos presentar a los alumnos la práctica de operaciones a través de juegos. Utilizar la imaginación de los niños es un muy buen recurso para entusiasmarlos en la realización de trabajos.
La presentación del trabajo a realizar puede ser a través de una pequeña historia, por ejemplo:
"Pedro es un chico al que le divierte inventar
rompecabezas los días de lluvia y muchísimas veces utiliza lo
aprendido en la clase de matemática para realizarlos.
Una de esas tardes de lluvia, estuvo trabajando en esa tarea,
recibió el llamado telefónico de un amigo y mientras conversaba
con él, su hermana de apenas 3 años borró algunos de los
números con los que Pedro había completado sus figuras, por
suerte en las primeras figuras escribió las cuentas empleadas
para armarlas.
¿Podrás ayudar a Pedro a completar las figuras con los números
que su hermana borró?".
Una vez completadas las figuras, es interesante aprovecharlas para afirmar conceptos espaciales: arriba, abajo, izquierda, derecha, región interior (adentro), región exterior (afuera).
Podemos plantear a los niños las siguientes preguntas:
¿En qué vértice del triángulo Pedro ubica el número que
resta? (Si el concepto de vértice no esta dado podemos hablar de
las puntas del triángulo)
¿En cuáles vértices Pedro ubica los números que suma?
¿Dónde ubica Pedro el resultado de la operación en cada
triángulo?
¿Hay números en la zona exterior del triángulo? ¿Puedes
describir su ubicación?.
Para trabajar con los alumnos:
Observemos las figuras que armó Pedro:
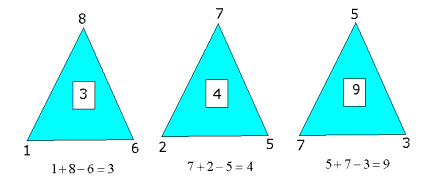
¿Puedes completar las
figuras en las que algunos números han sido borrados?
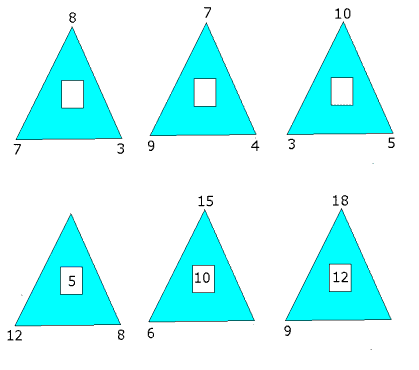
En este
tipo de trabajo se puede optar por una figura de mayor número de
lados, lo que permite trabajar con los alumnos una mayor
dificultad operatoria. Si se trabajan distintas figuras, luego de
completar el rompecabezas se trabaja la identificación de las
diferentes figuras.
Estoy segura de que la
creatividad de cada uno de ustedes sabrá encontrar en él una
alternativa interesante para realizarlo con sus alumnos.
Divisibilidad
Podemos trabajar este tema de la divisibilidad
numérica.
Es conveniente que ellos hayan adquiridos los
siguientes conceptos:
(Utilizo las definiciones para números naturales, pues esta
propuesta puede empezar a trabajarse en 2° ciclo del E.G.B).
Números primos: Un número es primo si sólo tiene dos divisores, el propio número y el 1.
Números compuestos: Todo número que no es primo.
¡ATENCIÓN! EL 1 NO ES PRIMO NI COMPUESTO, ES ESPECIAL.
Divisor común mayor:
El divisor común mayor de dos o más números, es el número
mayor que los divide exactamente, o sea el resto de la división
es cero.
Se lo llama con las iniciales, así: D.C.M.
Números coprimos o primos entre sí:
Dos números son coprimos o primos entre sí cuando sólo tienen
como divisor común mayor el 1.
Preguntémosle a nuestros alumnos si es posible confeccionar una regla de divisibilidad para cualquier número.
En la tabla de números primos y compuestos aparece el
criterio de divisibilidad para el número 12, puede resultar
interesante preguntarle a los niños por que dice: "Un
número es divisible por 12 cuando es divisible por 3 y por
4". Y por que no dice que un número es divisible por 12
cuando es divisible por 2 por 6.
Analicen con ellos algunos
múltiplos de 2 y de 6, que no lo son de 12,
Por ejemplo 18, 36, etc.
Seguramente los alumnos se
preguntarán por que se eligió ese par de número y no otro.
Si los alumnos no encuentran
solos la respuesta, podemos darles alguna pista recordando el
concepto de coprimos.
Luego trabajar todos juntos
la siguiente conclusión:
"Para encontrar la regla de divisibilidad de un número debes buscar las pareja de divisores primos entre sí (coprimos), si los tiene y de ellas elegir la formada por los números más grandes".
Es interesante trabajar con ellos ejercicios como los que
continúan:
1.
- No existe regla de divisibilidad del número 16. Observa:
Divisores de 16: {1, 2, 4, 8,16}
No tiene divisores primos entre sí.
- Si, existe regla de divisibilidad para 36. Observa:
Divisores de 36; {1, 2, 3, 4, 6, 9, 12, 18,36}
Parejas de factores primos entre sí: 2 y 9; 3 y 4; 4 y 9.
4 y 9 es la pareja elegida por que esta formada por los números
mayores, por lo tanto un número es divisible por 36 si es
divisible por 4 y por 9, a la vez.
- ¿Puedes escribir la regla de divisibilidad del número 56?, ¿y del número 30?
2.
Completa la siguiente tabla, siempre que sea posible:
|
Estas actividades en las cuales los
niños construyen las reglas, resultan muy enriquecedoras porque
los niños logran construir por si mismos las reglas de
divisibilidad de cualquier número, encontrando así, otras que
no son las más conocidas.
Les da la posibilidad de recurrir
menos a la memoria y más al razonamiento.
Espero encuentren en esta entrega
elementos para aplicar en sus clases.
Divisibilidad
Teniendo en cuenta la dificultad que observaba en los niños para simplificar fracciones, calcular m.c.m y m.c.d., factorear, etc., se puede usar una tabla con las reglas de divisibilidad, la cual se entrega a loss alumnos como material de consulta permanente que guardan en la sección "FICHAJE" de su carpeta, y podrá obtener muy buenos resultados. Comprobando que, poco a poco, los estudiantes van internalizando los criterios de divisibilidad.
Adjunto la tabla de ejercicios y problemas con diferentes grados de dificultad, con el objeto que los alumnos comprueben la utilidad de dicha tabla.
Sabemos que los niños necesitan verificar a través de su propia experiencia, porque esto realmente les simplifica la tarea; de lo contrario, el material entregado dormirá en el fondo de la mochila (en el mejor de los casos).
Divisible por: |
Criterio |
Ejemplo |
2 |
Un número es divisible por 2 cuando la cifra de las unidades es múltiplo de 2 (número par) | |
3 |
Un número es divisible por 3 si la suma de los valores absolutos de sus cifras es múltiplo de 3 | |
4 |
Un número es divisible por 4 cuando el número formado por las dos últimas cifras es múltiplo de 4 | |
5 |
Un
número es divisible por 5 cuando la cifra de las
unidades es múltiplo de 5 (0 ó 5) |
|
6 |
Un número es divisible por 6 cuando es divisible por 2 y por 3 |  |
7 |
Un número es divisible por 7 cuando la diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es múltiplo de 7 | 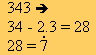 |
8 |
Un número es divisible por 8 cuando el número formado por las tres últimas cifras es múltiplo de 8 | 5888 1016 |
9 |
Un número es divisible por 9 si la suma de los valores absolutos de sus cifras es múltiplo de 9 | 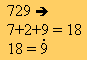 |
10 |
Un número es divisible por 10 si la cifra de las unidades es cero | 120 1540 250 1000 500 |
11 |
Un número es divisible por 11 cuando la diferencia entre la suma de los valores absolutos de las cifras de los lugares pares y la suma de los valores absolutos de los lugares impares, en el sentido posible, es múltiplo de 11 | 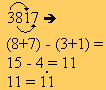 |
12 |
Un número es divisible por 12 cuando es divisible por 3 y por 4 | 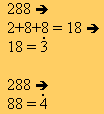 |
25 |
Un
número es divisible por 25 cuando el número formado por
las últimas dos cifras es múltiplo de 25 Un número es divisible por 25 si la cifra de las unidades más diez veces la cifra de las decenas es múltiplo de 25 |
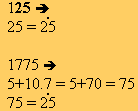 |
100 |
Un número es divisible por 100 si las últimas cifras son dos ceros | 2700 1700 25400 |
El juego de Nim
para tercer ciclo
El juego de Nim consiste en lo siguiente. Se ponen tres
montones de piedrecillas, uno con 3, otro con 4, otro con 5.
Juegan dos jugadores A y B. El primero en jugar, A, puede quitar
tantas piedras como quiera (siempre una o más) de uno sólo de
los tres montones. Luego juega B del mismo modo. Gana quien se
lleve la última piedra.
Tal vez te haya contado alguien la estrategia infalible que tiene
A. Se ponen en sistema binario los números de piedras de cada
montón. Al empezar estos son
3------------- 1 1
4------------- 1 0 0
5------------- 1 0 1
La estrategia consiste en quitar las piedras que haga falta del
montón adecuado para que los unos de cada columna de los
números en sistema binario sumen un número par. Así, aquí se
pueden quitar dos piedras del montón de 3 y queda
1------------- 1
4------------- 1 0 0
5------------- 1 0 1
El primer jugador gana necesariamente siguiendo esta misma
estrategia cada vez que le toque jugar.
¿Te has parado a pensar alguna vez por qué marcha? ¿Por qué A
puede llevar a cabo su estrategia haga B lo que haga? ¿Y si los
montones tienen números de piedras diferentes a 3, 4, 5?
Si lo averiguas no te será difícil tal vez dar con la
estrategia del juego de Moore, que es como el de Nim, pero
pudiendo quitar las piedras que se quiera (siempre una o más) de
uno o dos montones en cada turno.
Con los ojos cerrados. Consideremos ahora el juego
siguiente con un montón de 40 piedras. Los jugadores A puede
quitar 1,2,3,4, ó 5 piedras a su antojo. Luego B puede quitar
así mismo 1,2,3,4, ó 5 piedras. Ahora le toca a A. Gana quien
se lleve la última.
La estrategia de A consiste en dejar, siempre que no se pueda
llevar todas las piedras que quedan, un número de piedras que
sea múltiplo de 6. Es claro que así B no puede ganar, y como
gana alguien seguro, tiene que ser A quien gane. Una vez que A
conoce la estrategia, no le hace falta hacer cuentas más que la
primera vez que juega, en que quita 4 piedras, dejando 36. A
partir de entonces su táctica es sencilla: si B quita m, A quita
6-m.
Y además, con esto gano a aquel otro juego...
En un tablero de ajedrez se señalan dos cuadros A y B. ¿Es
posible pasearse con una torre por todo el tablero comenzando en
A y terminando en B? Recordemos que la torre se mueve horizontal
y verticalmente, nunca en oblicuo.
Por supuesto que uno piensa enseguida en lugar a lo mismo en un
tablero más pequeño, como en el juego del ajedrez recortado que
hemos visto antes y así resulta fácilmente que a veces, por
ejemplo en un tablero 2x2 con A y B en dos esquina diagonalmente
opuestas el paseo propuesto es imposible. Asimismo, quien conozca
el uso que en el otro juego hemos hecho de los colores, puede
pensar rápidamente en aplicar el mismo principio aquí. Si A y B
son del mismo color, blanco por ejemplo, el paseo es imposible en
el tablero 8x8. En efecto la torre va recorriendo sucesivamente
blanco, negro, blanco, negro,... Así si el paseo terminase en
blanco, el número de cuadros sería impar. En cambio será
imposible el paseo en un tablero con un número impar de cuadros
si A y B son de distinto color y también si son del mismo color
si es que este color es el más escaso en el tablero. ¿Podrías
dar con un teorema general y una estrategia para hacer el paseo
siempre que se pueda?